Stabilization by boundary feedback in 3D channel flow


Introduction
We stabilize the parabolic equilibrium profile in a 3D channel flow using actuators and sensors only at the wall. The feedback law uses tangential actuation (through teamed pairs of synthetic jets or rotating disks) and only local measurements of wall shear stress, allowing to embed the feedback in MEMS hardware, without need for wiring. The boundary feedback control law we use for the stabilization of a 3D channel flow is originated form our 2D channel flow work. These simulations require extensive computational effort especially as we apply our feedback control for channel flows with increasing Reynolds number. The time required to achieve stabilization is also increasing at the same time. This page will be updated as soon as I have the right equipment to obtain better results.

Current best result: stabilization of flow with Reynolds number: $ \Re e=4000 $ $ \left( \Re e_{\tau }\approx 160\right) $

The Equations with the Control

The periodic channel flow can be described by the 3D Navier-Stokes equations


$\displaystyle \mathbf W_{t}-\nu \Delta \mathbf W+(\mathbf W\cdot \nabla )\mathbf W+\nabla P$ $\displaystyle =$ $\displaystyle 0\textrm{ }\qquad \textrm{div}\mathbf W=0$  

where $ \mathbf W=\mathbf W(x,y,z,t)=(U(x,y,z,t),V(x,y,z,t),W(x,y,z,t))^{T} $ with steady state parabolic profile



\includegraphics {3dns.eps}



Boundary Control

Lyapunov analysis of the perturbation energy results in the energy inequality

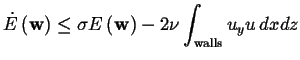
$\displaystyle \dot{E}\left( \mathbf w\right) \leq \sigma E\left( \mathbf w\right) -2\nu \int _{\text {walls}}u_{y}u\, dxdz$

that suggests boundary feedback control through tangential velocity actuation on the channel walls.


$\displaystyle U(x,-1,z,t)$ $\displaystyle =$ $\displaystyle K\left( U_{y}(x,-1,z,t)-\bar{U}_{y}\right)$  
$\displaystyle U(x,1,z,t)$ $\displaystyle =$ $\displaystyle -K\left( U_{y}(x,1,z,t)+\bar{U}_{y}\right)$  
$\displaystyle V(x,-1,z,t)$ $\displaystyle =$ 0  
$\displaystyle V(x,1,z,t)$ $\displaystyle =$ 0  
$\displaystyle W(x,-1,z,t)$ $\displaystyle =$ 0  
$\displaystyle W(x,1,z,t)$ $\displaystyle =$ 0  

i.e.,

$\displaystyle \left. U\right\vert _{\text {wall}}=K\left( \text {Wall\, Shear\,... ...ess}_{\text {measured}}-\text {Wall\, Shear\, Stress}_{\text {laminar}}\right) $

where $ K>0 $ is a control gain.

The way this boundary control adjusts the shear stress to that of the steady state profile is pictorial represented bellow.



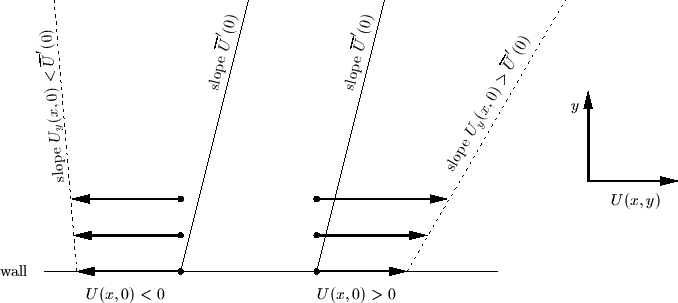
\rotatebox {90}{\includegraphics{actu1.ps}}



With the above control law we can prove the convergence of the flow to the steady state parabolic profile in $ L_{2} $, $ H^{1} $ and $ H^{2} $ Sobolev spaces.

Simulation Study

The only limitation in our theoretical result is that it is guaranteed only for sufficiently low values of the Reynolds number. Simulation results bellow demonstrate that the control law has a stabilizing effect far beyond the value required in the theorem.

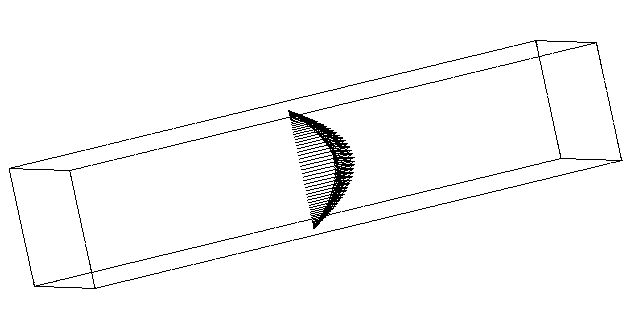
The direct numerical simulation was performed in a fully-developed turbulent channel flow with

  • Constant mass flux
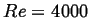
  • Reynolds number $ Re=4000 $
  • Channel dimensions $ 6\pi \times 2\times 3\pi $
  • hybrid Fourier pseudospectral-finite difference discretization
  • fractional step technique based on a hybrid Runge-Kutta/Crank-Nicolson time discretization

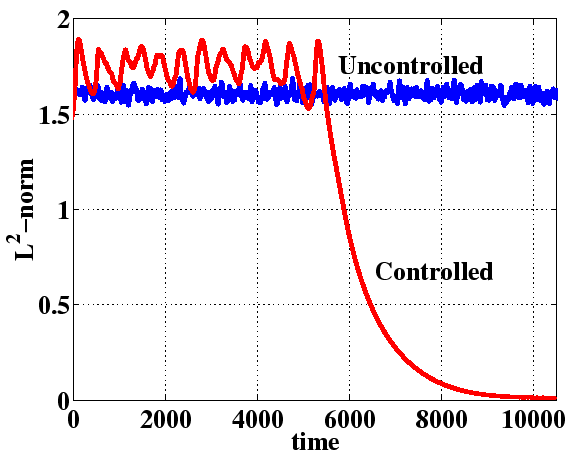
Perturbation Energy

The fact that our controller achieves stabilization is best expressed in terms of the $ L_{2} $-norm of the error between the steady state and the actual velocity field, the so called perturbation energy, which corresponds to system with $ k=0 $ (zero Dirichlet boundary conditions on the walls) in the uncontrolled case. There is a relatively large initial transient time before the effect of the control can be seen at around $ t=5500 $. What we see here is an interesting example of interaction between linear and nonlinear behavior in a dynamical system. Initially, when the velocity perturbations are large, and the flow is highly nonlinear, the energy input by the control increases the total energy. Later at about $ t=5500 $, the strong convective nonlinearities disappear, the controlled flow becomes close to laminar, and linear behavior dominates, along with its exponential energy decay.



\resizebox* {!}{10cm}{\includegraphics{l2.eps}}



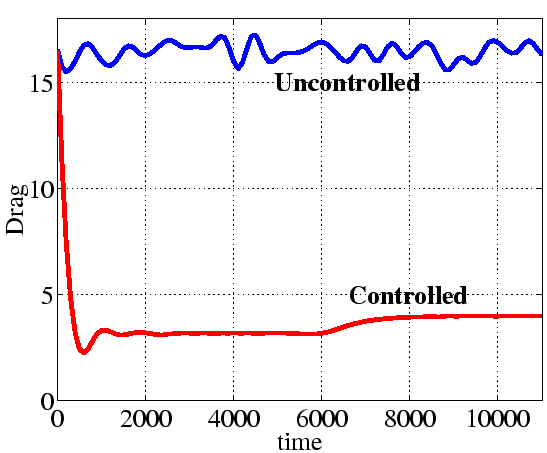
Instantaneous Drag

We obtain approximately $ 75\% $ drag reduction as a byproduct of our special control law. The drag in the controlled case ``undershoots'' bellow the value 4 (the level corresponding to the laminar flow) and eventually agrees with it up to two decimal places. It is striking that even though drag reduction was not an explicit control objective (as opposed to most of the works in this field), the stabilization objective results in a controller that reacts to the wall shear stress error, and leads to an instantaneous reduction of drag bellow the laminar level.



\resizebox* {!}{10cm}{\includegraphics{drag.eps}}



Discriminant

The discriminant of the velocity gradient tensor is a scalar quantity that is commonly used in visualizations to pinpoint vortex-type motions in the flow. In the following two pictures we show places where the discriminant has values larger than $ 0.9 $ at time $ t=4000 $. Due to our control law there are less vortical structures generated at the wall in the controlled case, although the controlled flow is far from being laminar at time $ t=4000 $ according to the perturbation energy plot. The flow is from the lower left to the upper right corner.



Uncontrolled ($ t=4000 $)
\includegraphics {discru.eps}
Controlled ($ t=4000 $)
\includegraphics {discrc.eps}



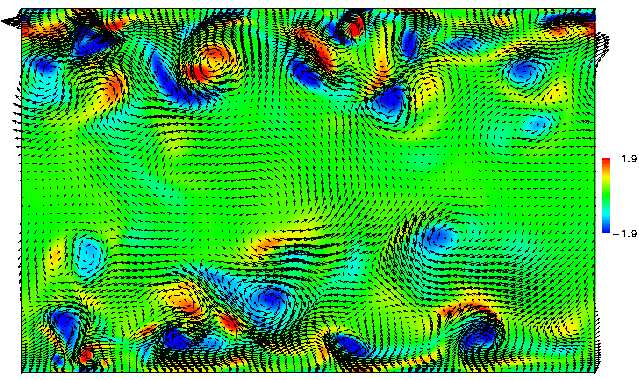
Spanwise Velocity and Streamwise Vorticity

Vortex structures generated at the wall eventually propagate into the interior of the domain where they dissipate. By adjusting the wall shear stress we decrease this vortex generation process. Note that the scale of the spanwise velocity vectors and streamwise vorticity in the controlled case is one fifth of the scale of those in the uncontrolled case.



Uncontrolled ($ t=5000 $)
\includegraphics {vortu.eps}
 
Controlled ($ t=5000 $)
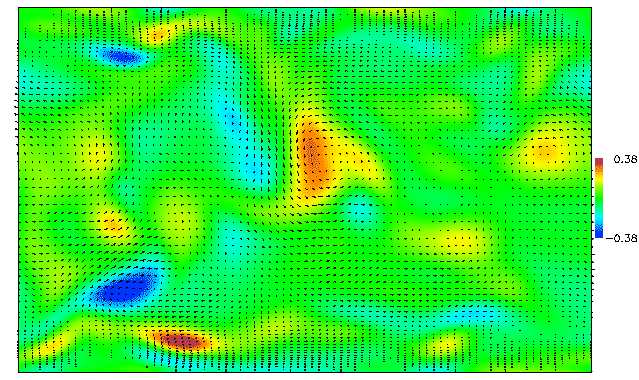\includegraphics{vortc.eps}



Maintained by Andras Balogh