(you gotta) Move Yourself

A 2d vector represents a direction and magnitude (length) in 2d space. In cartesian space, we store this as an x component and a y component which make a right triangle with the vector itself as the hypotenuse.

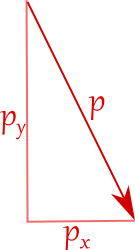
By assuming that the vector starts at the origin of the coordinate system, we can use vectors to represent the position of an entity in the 2d world.

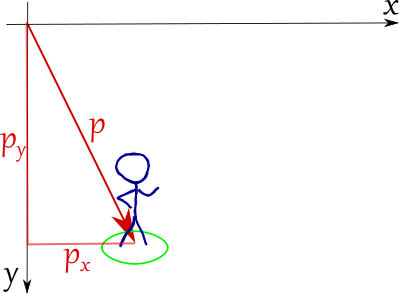
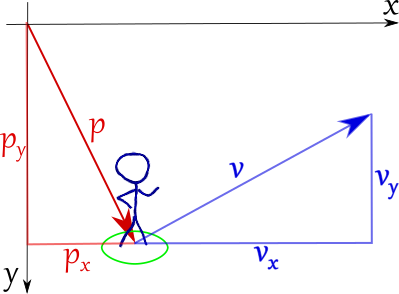
But wait! There's more! We can use the same vector class to represent the velocity of an entity by assuming that it starts at position of that entity.

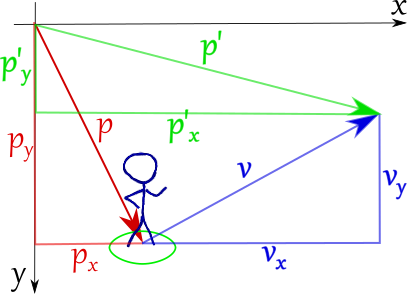
Vector addition is quite simple. As you can see below, adding two vectors together just means adding their x and y components independently. This means that our entity can move along that velocity vector by just adding it to its current position. In this case, v.y is negative, which works just fine.

p' = p + v

is just

p'.x = p.x + v.x
p'.y = p.y + v.y

If the magnitude of our velocity vector v is expressed in distance/millisec, then we have to multiply it by the amount of time that has passed, which brings us back to dat Euler.

p' = p + (v * delta)