Consider Burgers' equation
| (1) |
We achieve set point regulation:
where
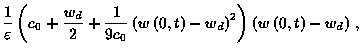 |
(2) | ||
 |
(3) |
The choice of ![]() at the boundary as the control input is motivated
by physical considerations. For example in thermal problems one cannot actuate
the temperature
at the boundary as the control input is motivated
by physical considerations. For example in thermal problems one cannot actuate
the temperature ![]() , but only the heat flux
, but only the heat flux ![]() . This makes the
stabilization problem nontrivial because homogeneous Neumann boundary conditions
make any constant profile an equilibrium solution, thus preventing not only
global but even local asymptotic stability. Even mixed linear boundary conditions
can introduce multiple stationary solutions.
. This makes the
stabilization problem nontrivial because homogeneous Neumann boundary conditions
make any constant profile an equilibrium solution, thus preventing not only
global but even local asymptotic stability. Even mixed linear boundary conditions
can introduce multiple stationary solutions.
Simulation Example
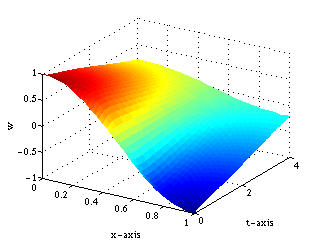
We consider first Burgers' equation with zero Neumann boundary condition (uncontrolled
system) with
![]() and with initial data
and with initial data
![]() and we regulate first to
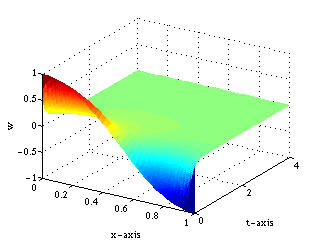
and we regulate first to ![]() (Figure 1) and then to
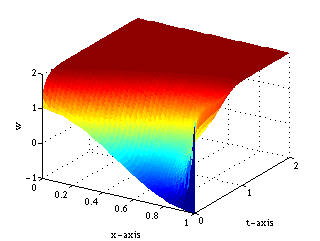
(Figure 1) and then to ![]() (Figure 2). The uncontrolled system is shown in Figure 1(a)
and 2(a). The solution exhibits slow convergence to the zero equilibrium
profile. (in fact, for some initial data, the numerical solution gets trapped
into this profile and never converges to zero. This unsatisfactory behavior
is remedied by applying boundary feedback, as shown in Figure 1(b).
(Figure 2). The uncontrolled system is shown in Figure 1(a)
and 2(a). The solution exhibits slow convergence to the zero equilibrium
profile. (in fact, for some initial data, the numerical solution gets trapped
into this profile and never converges to zero. This unsatisfactory behavior
is remedied by applying boundary feedback, as shown in Figure 1(b).
Click on the images to see animation!